Recognizing the profound impact of analog techniques on students' understanding of physical systems and their mathematical principles, Reswick proposed the creation of a "dormitory computer" tailored for student use. This innovative device was designed to provide each student with a portable unit that would allow them to experiment at their convenience and in any location. Crucially, the computer would not require any special expertise to use. Thus, the culmination of Reswick's vision materialized in the form of the Personal Analog Computer.
Defining Analog Computers
Analog computers are computing devices that use continuous physical phenomena, such as electrical voltages or mechanical motion, to represent and solve mathematical problems. Unlike digital computers, which process discrete data in binary form, analog computers work with continuously variable signals. These machines excel at solving differential equations and simulating dynamic systems, making them particularly valuable for tasks involving real-time simulation, control systems, and scientific modeling. While they have largely been replaced by digital computers in mainstream computing, analog computers continue to find niche applications in fields where their unique capabilities offer advantages over digital counterparts.
Exploring the Personal Analog Computer: A Versatile Tool for Mathematical Visualization
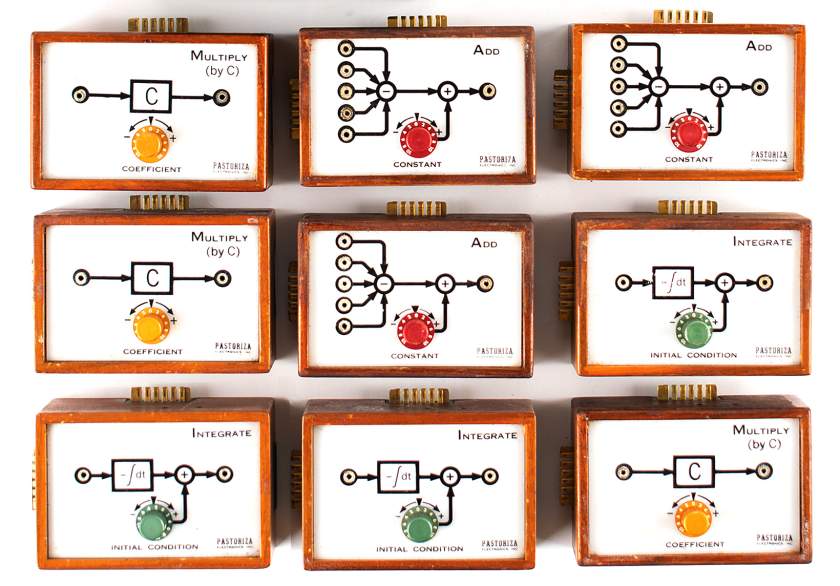
The Personal Analog Computer (PAC) is a testament to the convergence of innovative technology and educational advancement. It serves as an electronic demonstration system using miniature analog computer modules, each designed to visually represent and solve mathematical equations. These modules are capable of performing three basic mathematical operations: addition, multiplication by a constant, and integration.
The beauty of the PAC is its versatility. By strategically combining these modules and adjusting their parameters, a variety of complex physical systems can be effectively simulated. In addition, students are able to monitor and plot the behavior of system variables, gaining invaluable insight into the dynamic nature of mathematical models.
The purpose behind the development of Personal Analog Computer
The genesis of the modular PAC system stems from a fundamental educational objective: to bridge the gap between dynamic physical systems and their mathematical representations. Designed with careful attention to pedagogical effectiveness, the PAC system serves as an intermediary model that facilitates a deeper understanding of the intricate relationship between real-world phenomena and mathematical abstractions.
For students embarking on the journey of understanding, the PAC system offers a transformative learning experience. Once armed with an understanding of the physical intricacies of a system and the underlying differential equations that govern its behavior, students can seamlessly translate their knowledge into tangible simulations using PAC units. These units faithfully replicate the real-time behavior of system variables, allowing students to engage in hands-on experimentation at their convenience and in any location.
In essence, the PAC system serves as more than a technological marvel; it is a catalyst for experiential learning. By allowing students to interact directly with mathematical models in a tangible way, the PAC system not only strengthens their understanding of physical and mathematical principles, but also fosters a deeper appreciation for the symbiotic relationship between theory and practice. As such, the PAC system becomes an indispensable tool in the arsenal of modern educational methodologies, poised to inspire generations of curious minds to explore the boundless realms of mathematical inquiry.
Personal Analog Computer Specifications
PAC Modules:
The Personal Analog Computer (PAC) has four distinct modules: the ADDER, INTEGRATOR, COEFFICIENT MULTIPLIER, and CONTROL UNIT, each carefully designed to perform specific mathematical functions.
Accuracy:
With a remarkable accuracy rate of 1%, the PAC ensures reliable and precise calculations in various mathematical operations.
Graphical panels:
To enhance the user experience, each module has a graphic panel surface that vividly illustrates its mathematical operation. These white-decorated panels provide a convenient surface for marking with pencils.
Connectivity:
For seamless operation, the units are physically and electrically interconnected via four gold-plated connectors that efficiently transfer power and control signals.
Variable Connectivity:
Navigating mathematical complexities is made effortless with miniature banana patch cords that allow variables to be connected with unparalleled ease.
Parameter Adjustment:
Tailoring calculations to specific needs is a breeze with front-panel controls that allow users to adjust parameters with precision and finesse.
Portable Power:
Equipped with a portable power supply housed in the control unit, the PAC ensures uninterrupted functionality in a variety of environments.
Readout Display:
Navigating through calculations is made easy with a large, center-positioned precision meter that allows users to measure any variable with ease and accuracy.
Using the Personal Analog Computer
In exploring the Personal Analog Computer (PAC), we encounter Figure 1, which illustrates a typical physical system ripe for analysis-the configuration of a spring and a mass. Here, users attempt to dissect the intricacies of this system to gain insight into its behavior and dynamics.
The defining parameters of the system include the spring constant, with the mass conveniently assumed to be 1 for simplicity. Central to the analysis are the variables 'x', which represents the displacement, and 'F', which represents the force exerted between the mass and the spring.
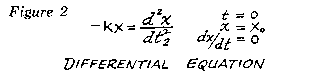Moving on to Figure 2, the user is presented with the differential equations that are critical to understanding the system. These equations are written to include the initial position of the mass, which is displaced by an amount denoted by 'X0'.
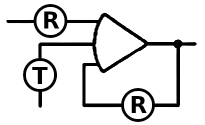
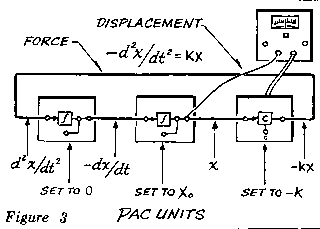Moving on to Figure 3, we encounter the interconnection layout of the PAC units - an integral aspect of the analytical process. Here, each patch cord symbolizes a variable, while each box represents a mathematical operation. Specifically, users configure the coefficient multiplier to match the spring constant, set the middle integrator to "X0" as the initial condition, and position the first integrator to zero, indicating an initial velocity of zero.
The user initiates the analysis process by pressing the SET button to set the initial parameters. Then, by pressing the HOLD switch, the problem is started, causing the "X" variables to track the sine wave shown in the accompanying graph. Conversely, pushing the HOLD switch up facilitates problem execution at one-second intervals.
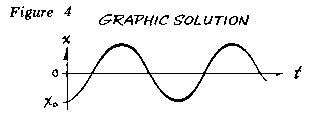Figure 4 provides clarity on stopping the analysis process, with the HOLD switch in the neutral position freezing the problem and allowing the user to take readings and plot variables. This culminates in the generation of a comprehensive graphical solution that provides users with invaluable insight into the behavior of the system being analyzed.
Exploring the Components of the Personal Analog Computer (PAC)
Within the confines of the Personal Analog Computer (PAC) lie meticulously crafted arithmetic units consisting of sophisticated electronic circuitry designed to exacting standards. Each unit houses an operational amplifier with an open-loop gain of 1,000, augmented by meticulously designed feedback components tailored to perform the required arithmetic operations with precision. Prior to deployment, rigorous testing and calibration procedures ensure that each unit achieves better than 1% accuracy.
The Pastoriza Personal Analog Computer, manufactured in 1963 by Pastoriza Electronics, Inc. of Boston, Massachusetts, is a vintage marvel of computer technology. Encased in its original leather carrying case, the 13" x 5.25" x 11.5" computer bears distinctive gold lettering on the front, proudly proclaiming "Personal Analog Computer" and "Pastoriza Electronics, Inc., Boston 16 Mass.". The compact, battery-operated computer consists of a control unit, nine configurable modular units, and eight connecting cables. The control unit, which measures 13.3 x 6.4 x 17.8 cm (5.25" x 2.5" x 7"), includes essential components such as a counter and on/off, set and hold switches for seamless operation. The nine modular units, each measuring 10.2 x 4.5 x 7 cm (4" x 1.75" x 2.75"), are divided into three "Add", three "Multiply (by C)", and three "Integrate" components, distinguished by bright red, yellow, or green dials. Beneath each unit is a labeled bottom, identified by numbers such as "231," "238," "240," or "241. Notably, the bottom of the control unit bears the number "241". Completing the ensemble are eight black connecting wires ranging from 5.5" to 25" in length, which facilitate seamless interconnection between components for extensive computational endeavors.
The standard complement of PAC units, however, included two integrators, two coefficient multipliers, an adder, and a control unit, providing a comprehensive arsenal for mathematical exploration and analysis. Beyond their utility in tackling conventional first- and second-order differential equations, PAC units find application in elucidating solutions to nonlinear differential equations and in illuminating the behavior of nonlinear circuits, including but not limited to flip-flops, multivibrators, and waveform generators. In addition, these devices serve as invaluable tools for conducting a wide variety of numerical experiments, enriching the educational experience with hands-on exploration and discovery.
As a side note, this Pastoriza Personal Analog Computer, originally tailored for students at Case Institute of Technology, served as a pioneering educational tool during a transformative era in computing history. Notably, Case Institute of Technology merged with Western Reserve University in 1967, creating Case Western Reserve University, which proudly hosted the first ABET-accredited program in computer engineering. Records indicate that in late 1962 or early 1963, approximately 200 students were provided with these computers by the institution for integration into their linear systems course. This initiative was part of a study to compare the academic performance of students equipped with slide rules to those using the innovative analog computer. Under the direction of Dr. James Reswick, then head of the Case Engineering Design Center, the design and manufacturing effort was led by James Pastoriza, for whom the computers were named. Notably, George Philbrick, a prominent figure in analog computer systems, contributed his expertise to the project, cementing the legacy of the Pastoriza Personal Analog Computer as a collaborative effort at the forefront of educational innovation. Last but not least, Pastoriza Electronics also made the first high-precision switched digital-to-analog converter in computer history. Pastoriza Electronics was later acquired by Analog Devices in 1969.
The Last Era of Analog Computers
The evolution of computing technology has witnessed the gradual decline of analog computers, ushering in the dominance of their digital counterparts. However, it is important to recognize the critical role that analog computers played, particularly in fostering a deeper understanding of mathematical principles and facilitating hands-on experimentation in educational settings. While digital computing reigns supreme in today's computing landscape, the legacy of analog computers remains as a testament to their lasting impact on computational science and engineering. So as we say goodbye to the last era of analog computers, we remember their contributions to the rich tapestry of technological advancement and educational innovation.
Further reading on analog computers:
. Additional info on Pastoriza Electronics.
. "Opportunities in Physical Computing driven by Analog Realization", by Jennifer Hasler, Georgia Institute of Technology, Atlanta
. "Modern Analog Computer Schematics", The Analog Thing
